Isogeometric Analysis: NURBS curves and surfaces in Octave and TypeScript

In this blog post I wrote some notes about B-splines. There are however important classes of curves and surfaces that cannot be represented by piecewise-polynomials like circles, ellipses etc... NURBS come to the rescue.

NURBS curves

NURBS is a generalization of B-splines where basis functions are defined with piecewise-rational polynomials. Again the parametric domain is split into multiple ranges by using a knot vector. The general definition is:

$$\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}R_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i},\;a\leq\xi\leq b$$
$\boldsymbol{P}_{i}$ are the control points and the functions $R_{i}^{p}$ are the NURBS basis functions, defined as:

$$R_{i}^{p}\left(\xi\right)=\dfrac{N_{i}^{p}\left(\xi\right)w_{i}}{{\displaystyle\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}},\;a\leq\xi\leq b,$$
where the functions $N_i^{p}$ are the B-spline basis functions (defined here):

$$N_{i}^{0}\left(\xi\right)=\left\{ \begin{array}{ll}1, & \xi_{i}\leq\xi<\xi_{i+1}\\0,&\text{otherwise}\end{array}\right.,a\leq\xi\leq b$$ $$N_{i}^{p}\left(\xi\right)=\frac{\xi-\xi_{i}}{\xi_{i+p}-\xi_{i}}\cdot N_{i}^{p-1}\left(\xi\right)+\frac{\xi_{i+p+1}-\xi}{\xi_{i+p+1}-\xi_{i+1}}\cdot N_{i+1}^{p-1}\left(\xi\right),a\leq\xi\leq b$$
and the values $w_i$'s are known as weights. The knot vector has the same definition given for B-spline curves:

$$\Xi=\left[\underset{p+1}{\underbrace{a,\ldots,a}},\xi_{p+1},\ldots\xi_{n},\underset{p+1}{\underbrace{b,\ldots,b}}\right],\;\left|\Xi\right|=n+p+2,$$

NURBS surfaces

By using the tensor product we can obtain definitions for NURBS in spaces of higher dimension. For surfaces, given the knot vectors:

$$\Xi=\left[\underset{p+1}{\underbrace{a_{0},\ldots,a_{0}}},\xi_{p+1},\ldots,\xi_{n},\underset{p+1}{\underbrace{b_{0},\ldots,b_{0}}}\right],\left|\Xi\right|=n+p+2$$ $$H=\left[\underset{q+1}{\underbrace{a_{1},\ldots,a_{1}}},\xi_{q+1},\ldots,\xi_{m},\underset{q+1}{\underbrace{b_{1},\ldots,b_{1}}}\right],\left|H\right|=m+q+2$$
a NURBS surface can be defined as:

$$\boldsymbol{S}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}R_{i,j}^{p,q}\left(\xi,\eta\right)\boldsymbol{P}_{i,j},\;\left\{ \begin{array}{c}a_{0}\leq\xi\leq b_{0}\\a_{1}\leq\eta\leq b_{1}\end{array}\right.$$
where:

$$R_{i,j}^{p,q}\left(\xi,\eta\right)=\dfrac{N_{i}^{p}\left(\xi\right)N_{j}^{q}\left(\eta\right)w_{i,j}}{{\displaystyle \sum_{\hat{i}=0}^{n}\sum_{\hat{j}=0}^{m}N_{\hat{i}}^{p}\left(\xi\right)N_{\hat{j}}^{q}\left(\eta\right)w_{\hat{i},\hat{j}}}},\;\left\{ \begin{array}{c}a_{0}\leq\xi\leq b_{0}\\a_{1}\leq\eta\leq b_{1}\end{array}\right.$$
and $w_{i,j}$ is the weight.

Homogeneous Coordinates

The implementations found in the repo do not directly implement the summations above, but use instead homogeneous coords to make calculations simpler. Let's consider the general form of a B-spline curve:

$$\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i},\;a\leq\xi\leq b$$
Control points $\boldsymbol{P}_i$ can be written in homogeneous coords like this:

$$\boldsymbol{P}_{i}^{w}=\left[\begin{array}{c} x_{i}\\ y_{i}\\ z_{i}\\ 1 \end{array}\right]$$
We can multiply each control point by a value $w_i\neq 0$, and the result would still represent the same point in the euclidean space. As a result, we can write:

$$\boldsymbol{C}^{w}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\cdot\left[\begin{array}{c} x_{i}w_{i}\\ y_{i}w_{i}\\ z_{i}w_{i}\\ w_{i} \end{array}\right]=\left[\begin{array}{c} \sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)x_{i}w_{i}\\ \sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)y_{i}w_{i}\\ \sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)z_{i}w_{i}\\ \sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i} \end{array}\right]$$
$\boldsymbol{C}^w(\xi)$ is therefore the original B-spline curve in homogeneous coords. Now we can map back it to the euclidean space:

$$\boldsymbol{C}\left(\xi\right)=\left[\begin{array}{c} \frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)x_{i}w_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}\\ \frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)y_{i}w_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}\\ \frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)z_{i}w_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}\\ 1 \end{array}\right]$$
which yields:

$$\boldsymbol{C}\left(\xi\right)=\frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}\boldsymbol{P}_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}$$
This means that, moving to homogeneous coords, we can use a simpler form. Given:

$$\boldsymbol{P}_{i}^{w}=\left[\begin{array}{c} x_{i}w_{i}\\ y_{i}w_{i}\\ z_{i}w_{i}\\ w_{i} \end{array}\right]$$ we can write a NURBS curve as:

$$\boldsymbol{C}^{w}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i}^{w}$$
and a NURBS surface as:

$$\boldsymbol{S}^{w}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}N_{i}^{p}\left(\xi\right)N_{j}^{q}\left(\eta\right)\boldsymbol{P}_{i}^{w}$$
All the implementations in the repo use these simpler forms.

Octave Implementation

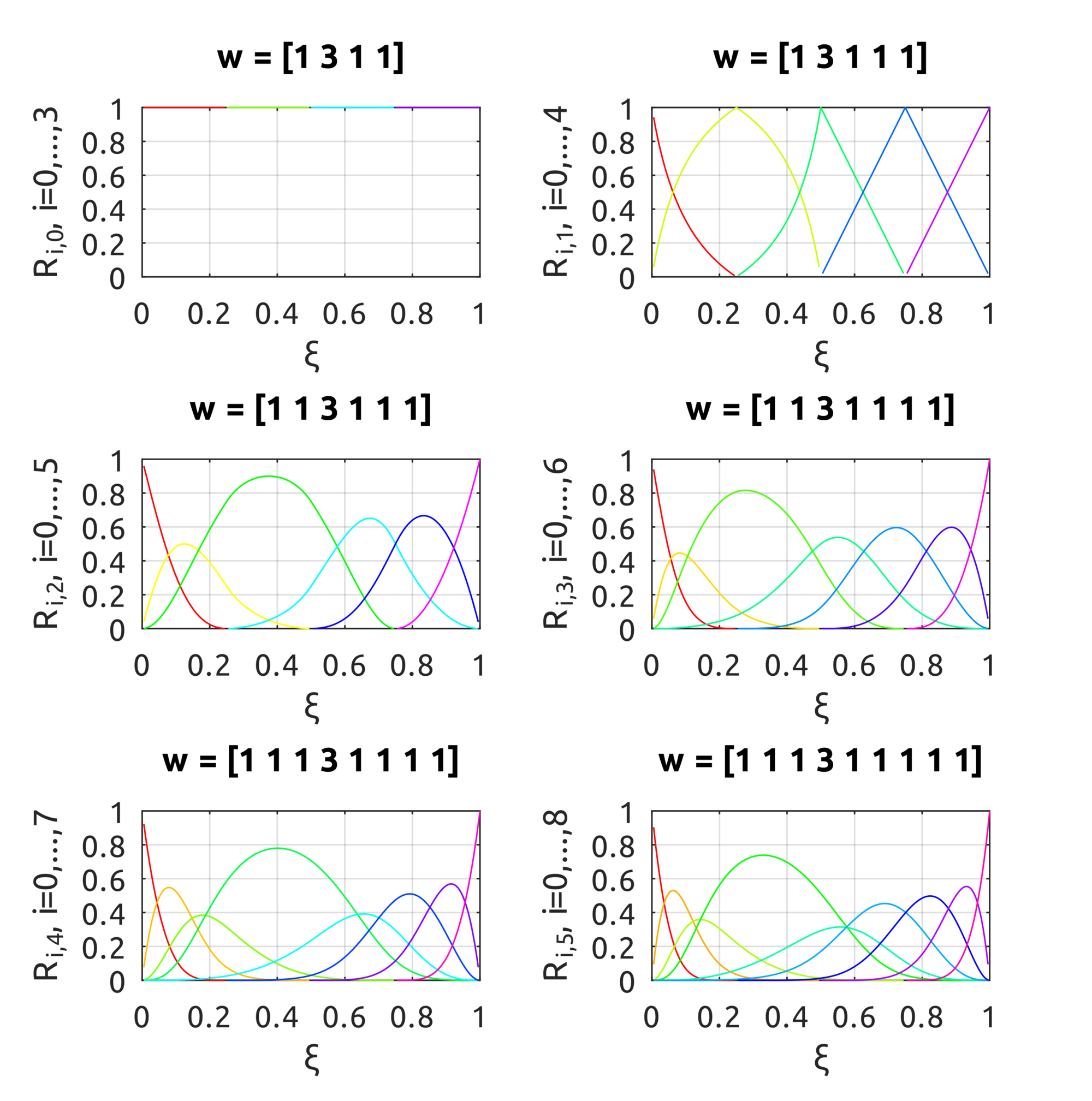
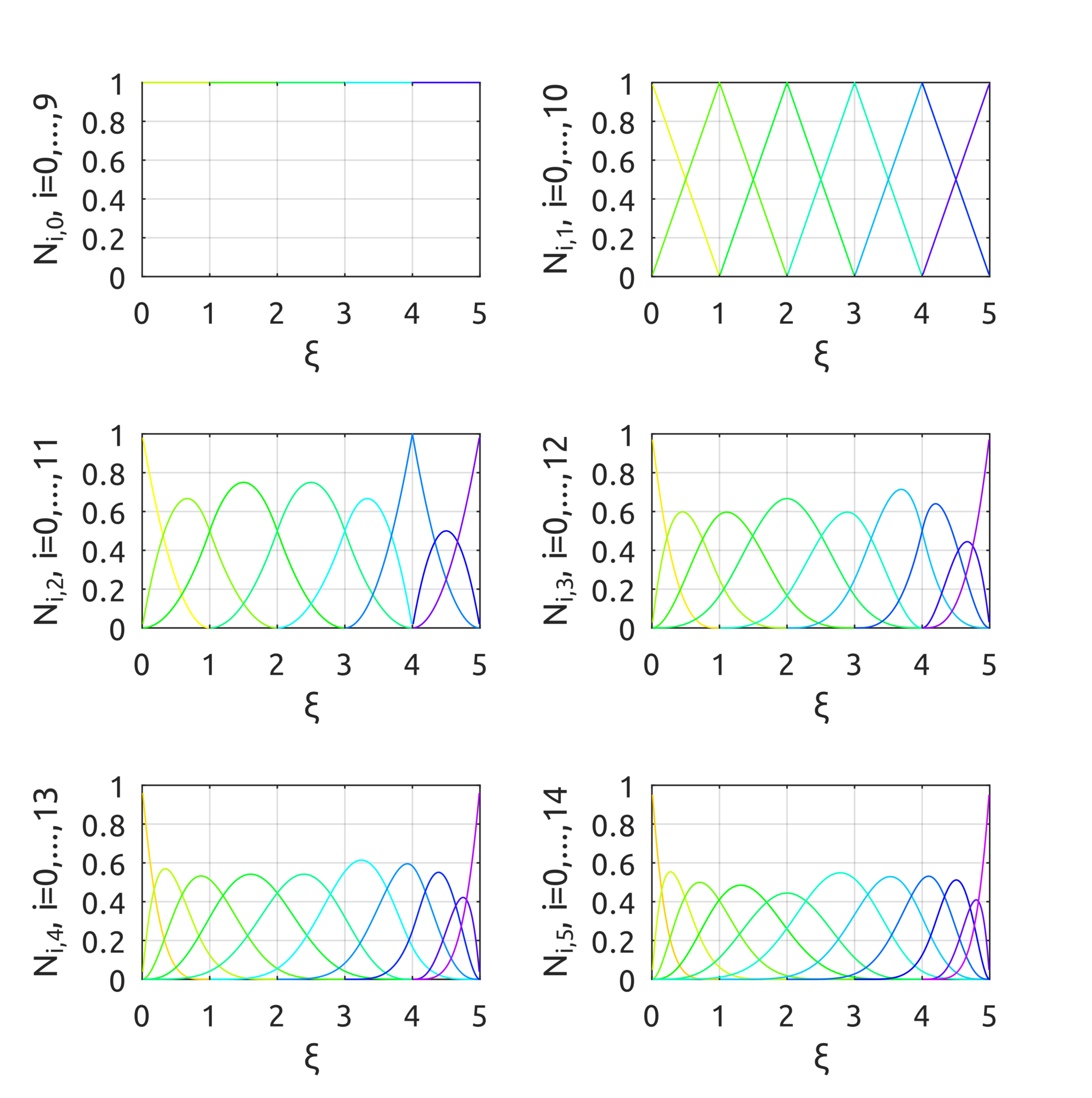
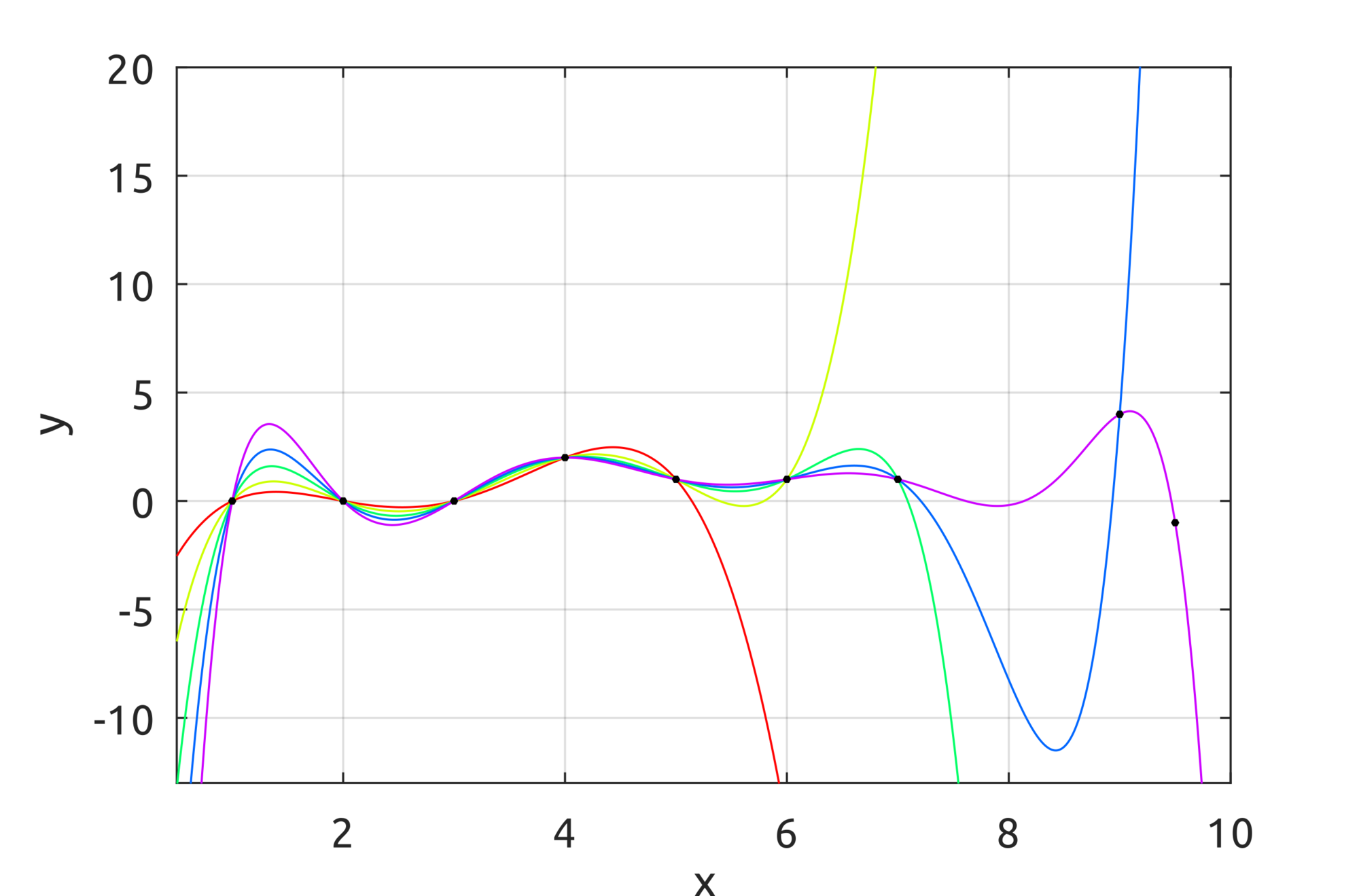
The computeNURBSBasisFun script can be used to compute NURBS basis functions. The drawNURBSBasisFunsP5 draws:

in the plots the effect of the weight is pretty clear. From top to bottom, the degree of the basis funs is increased over the knot vector $ Xi = [0.25, 0.5, 0.75]$.
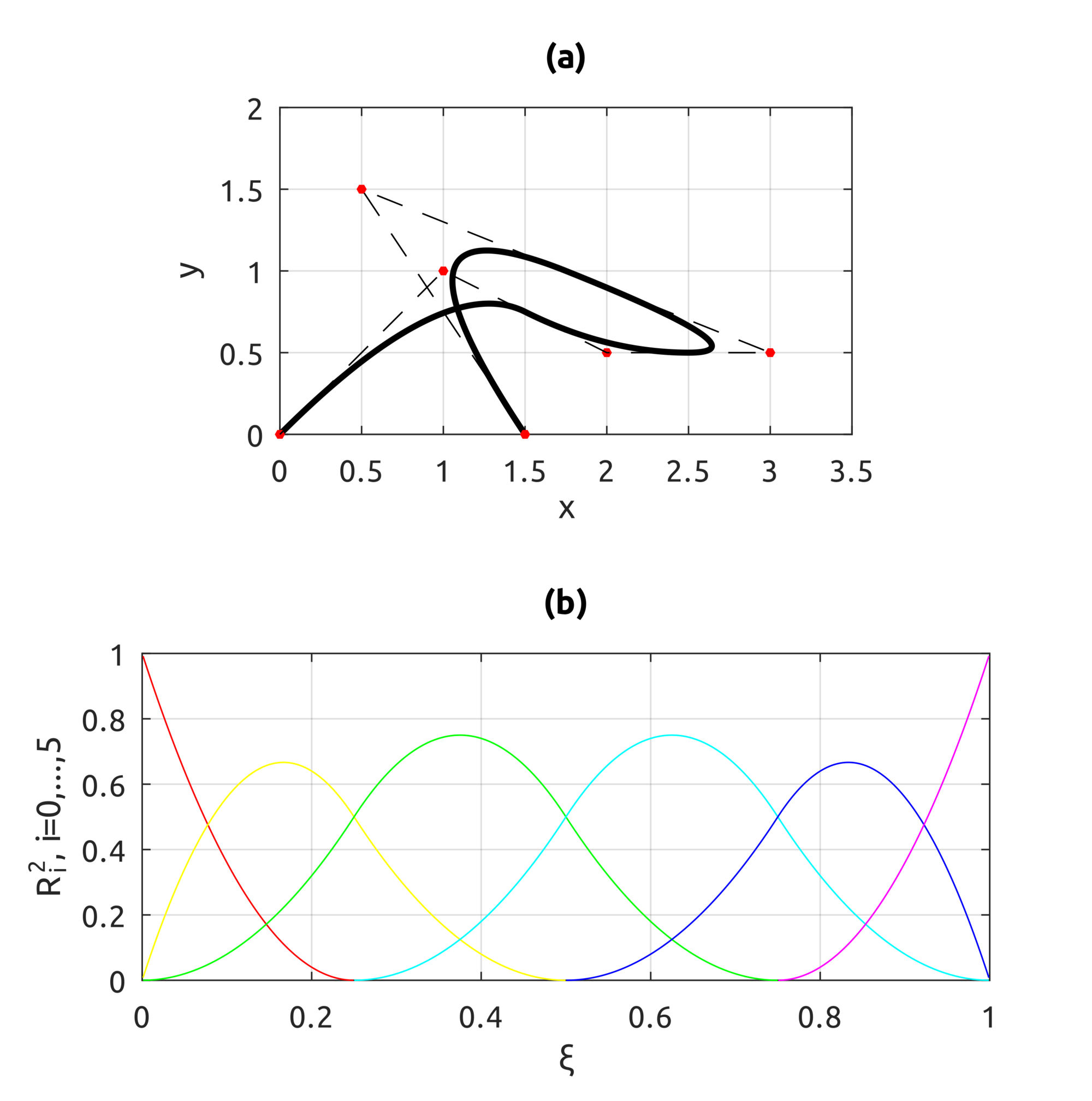
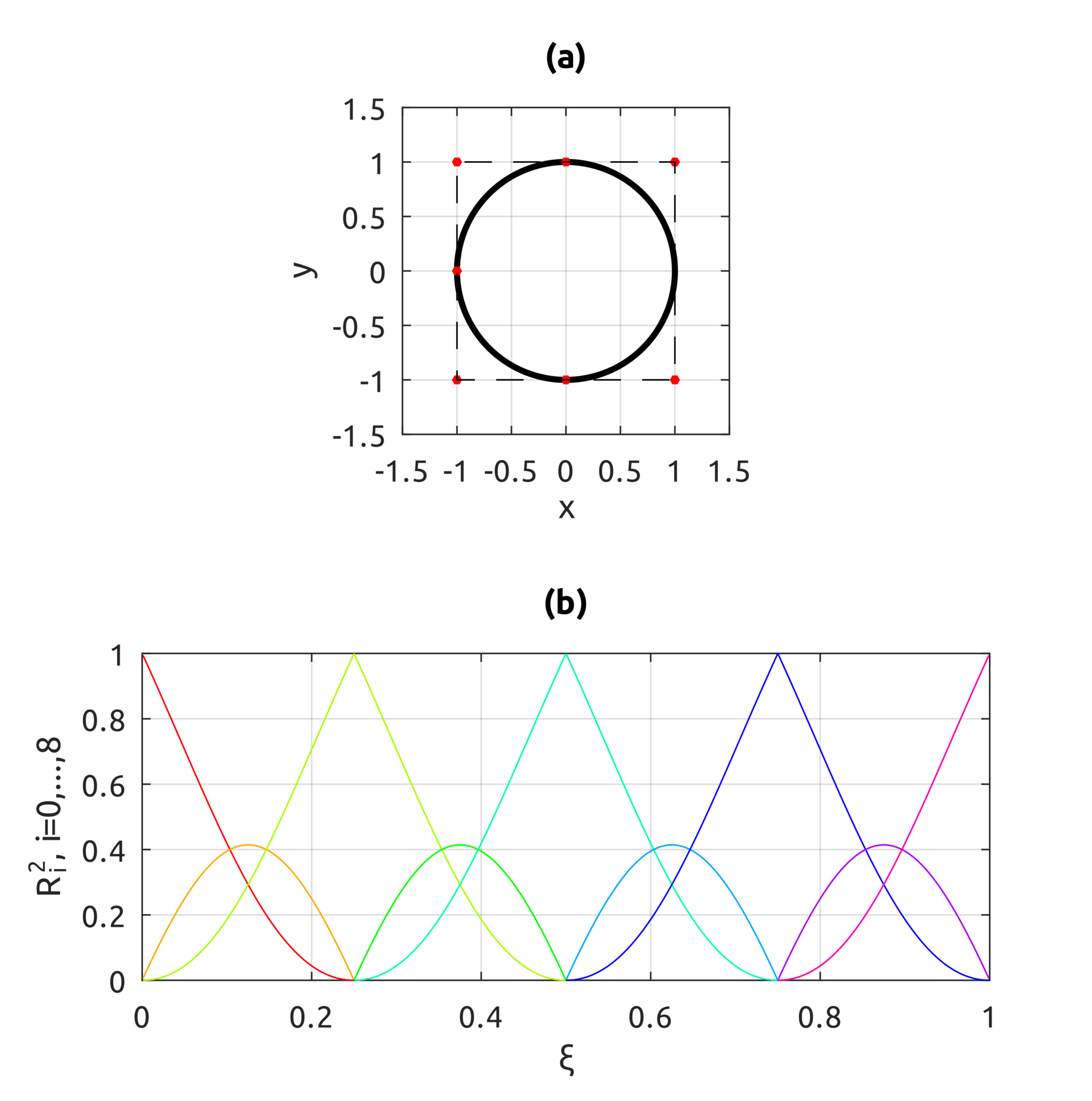
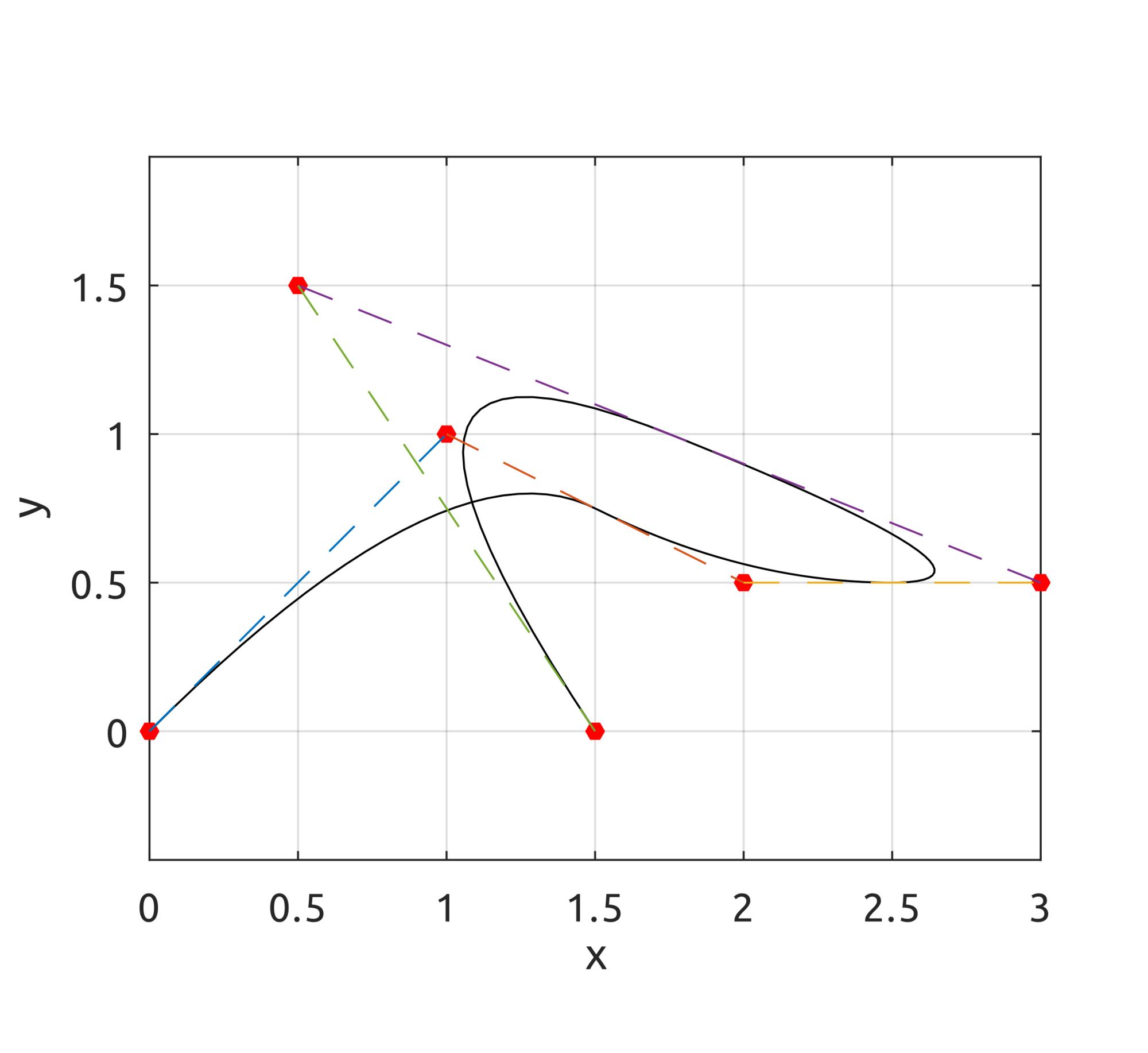
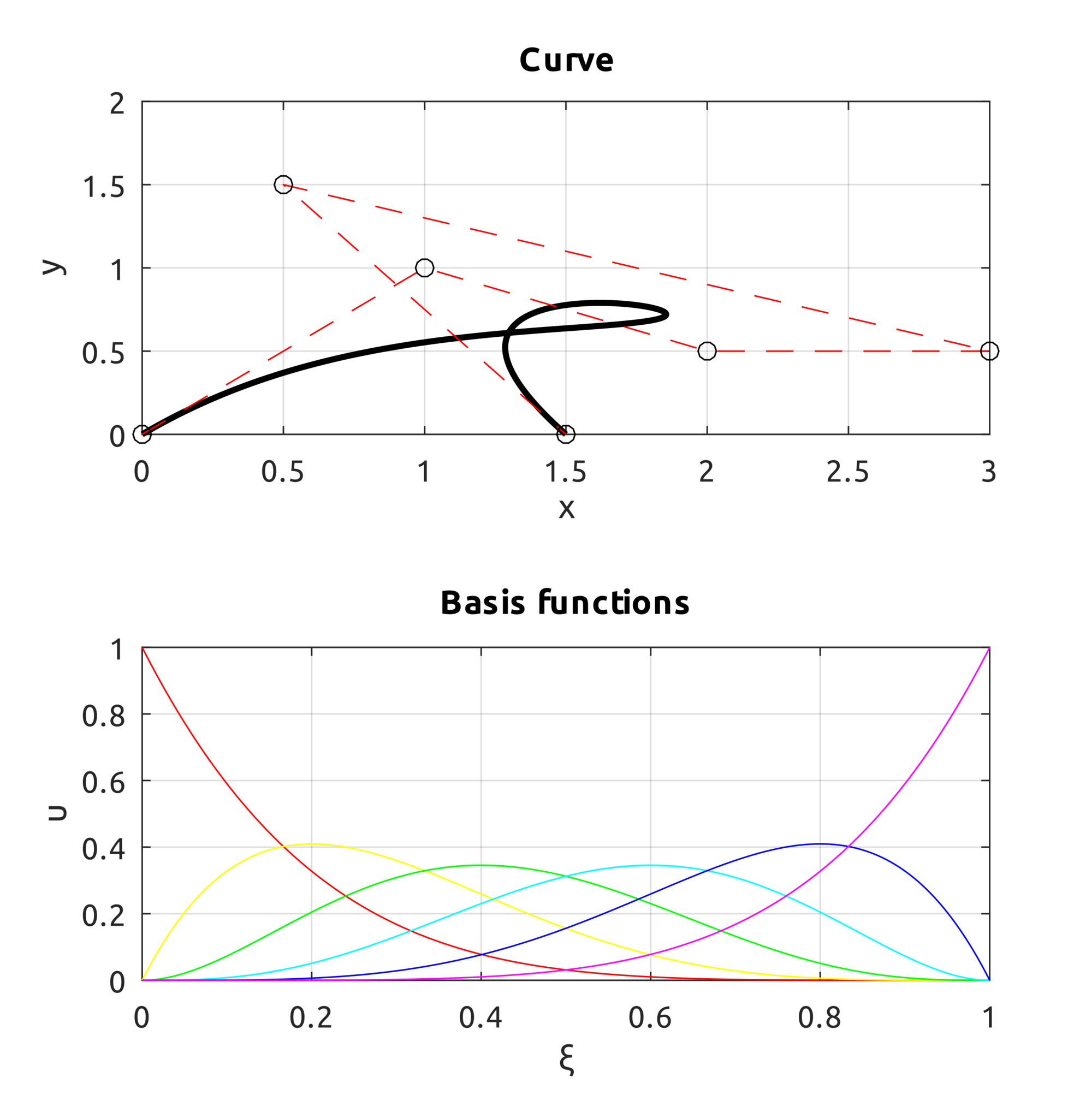
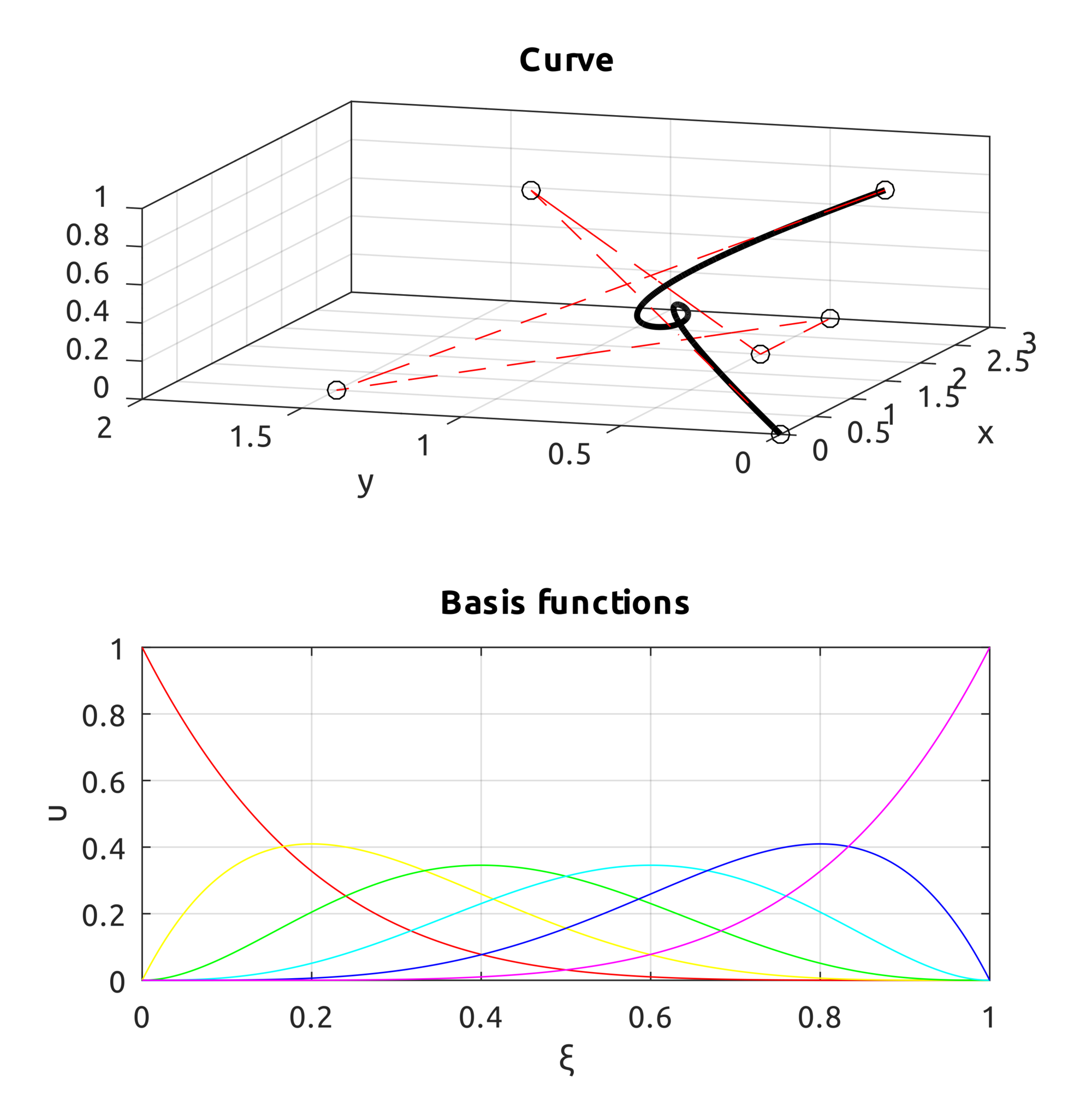
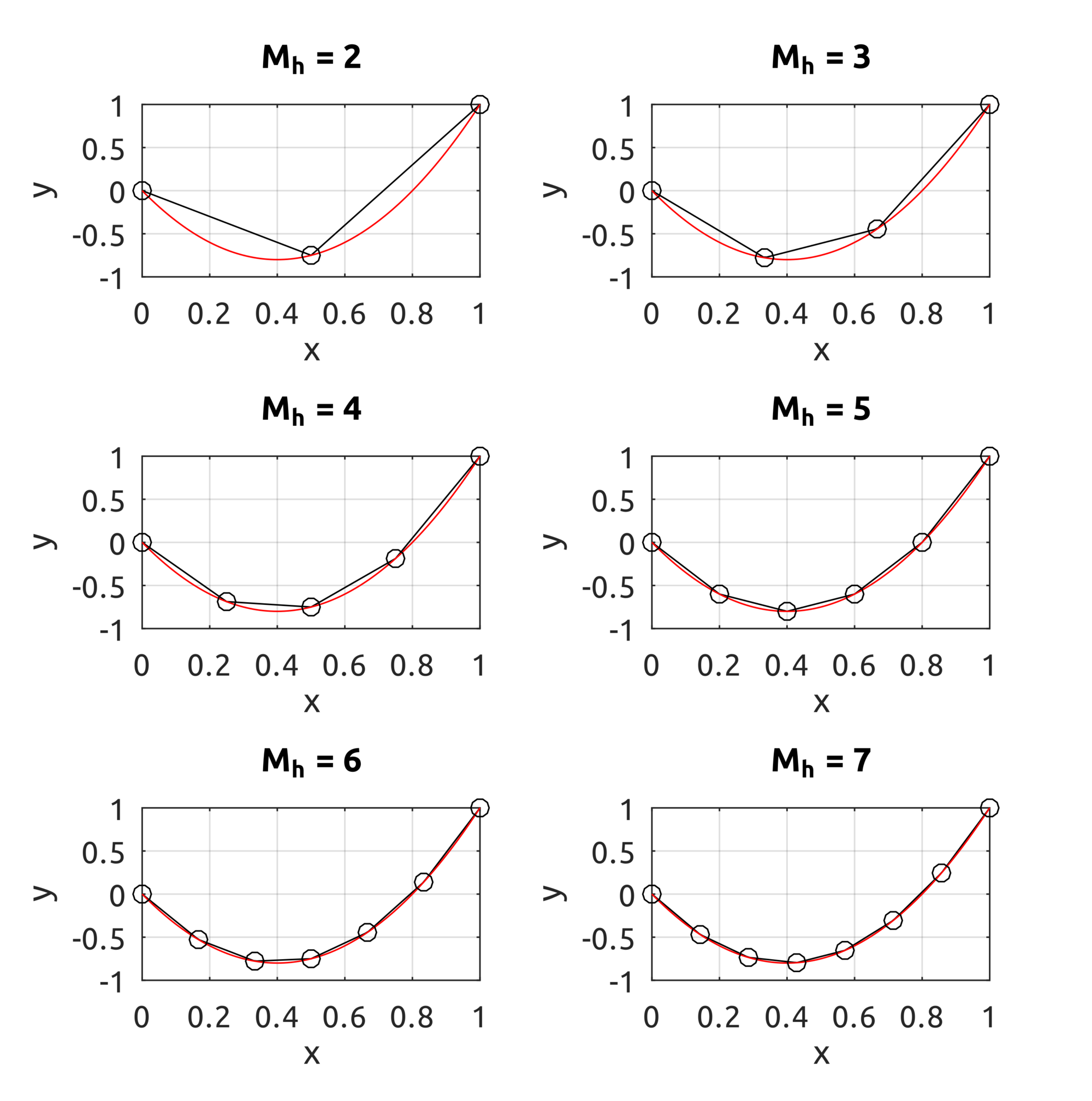
The computeNURBSCurvePoint script uses homogeneous coords to compute a NURBS curve using B-spline basis functions. We can build curves similar to what we could draw with B-splines but we can also draw circles:

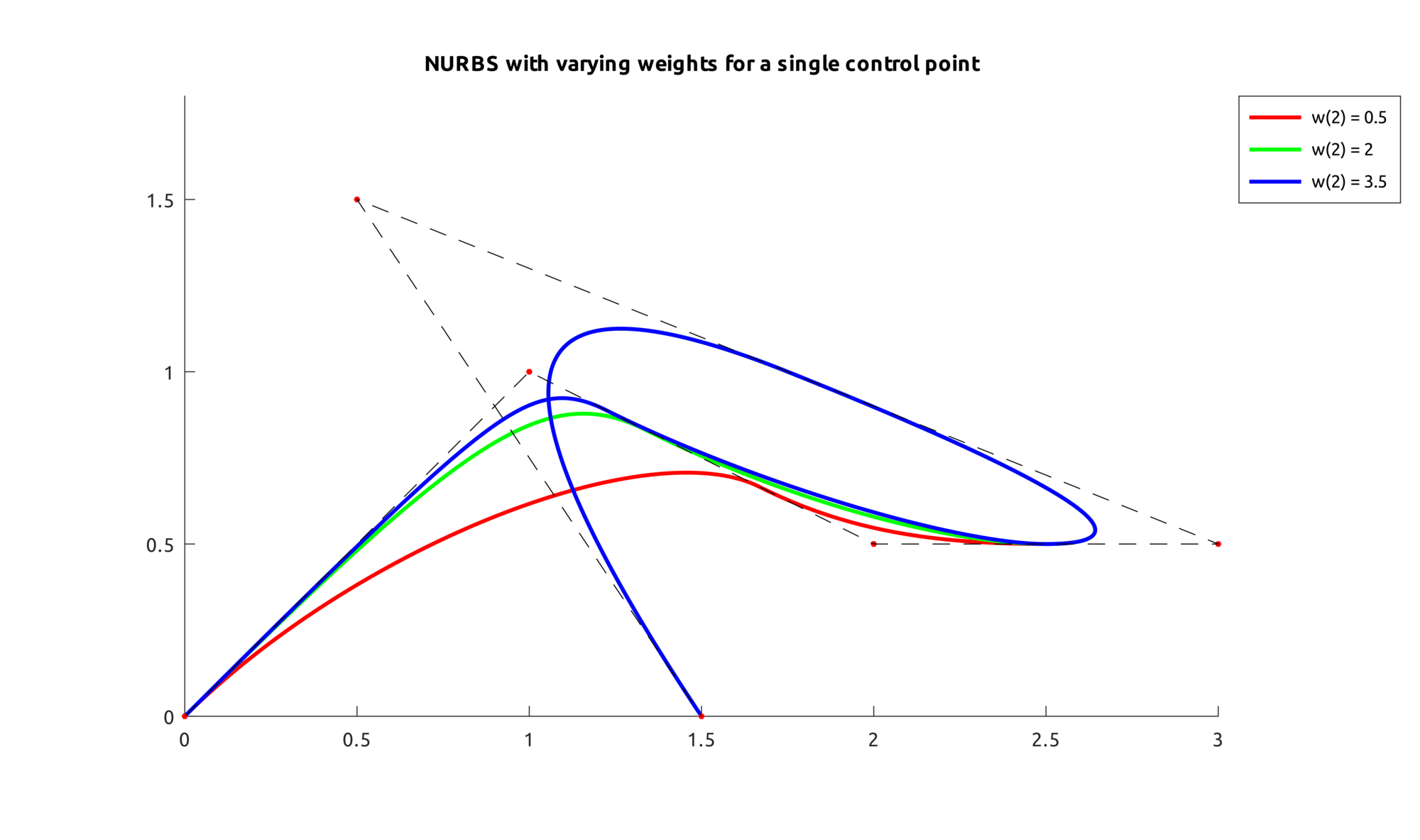
This is an example that shows what happens when a weight is increased on one point:

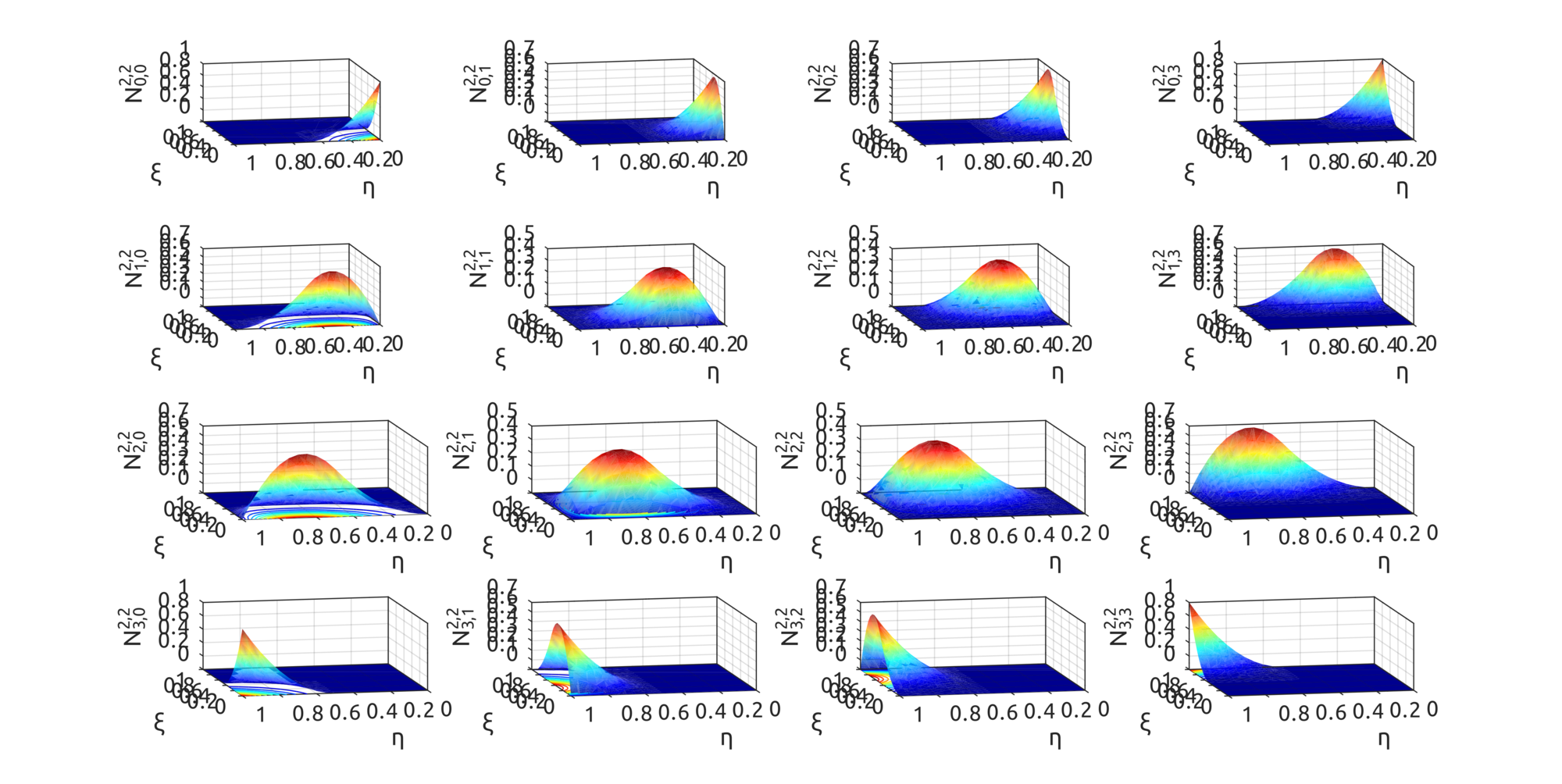
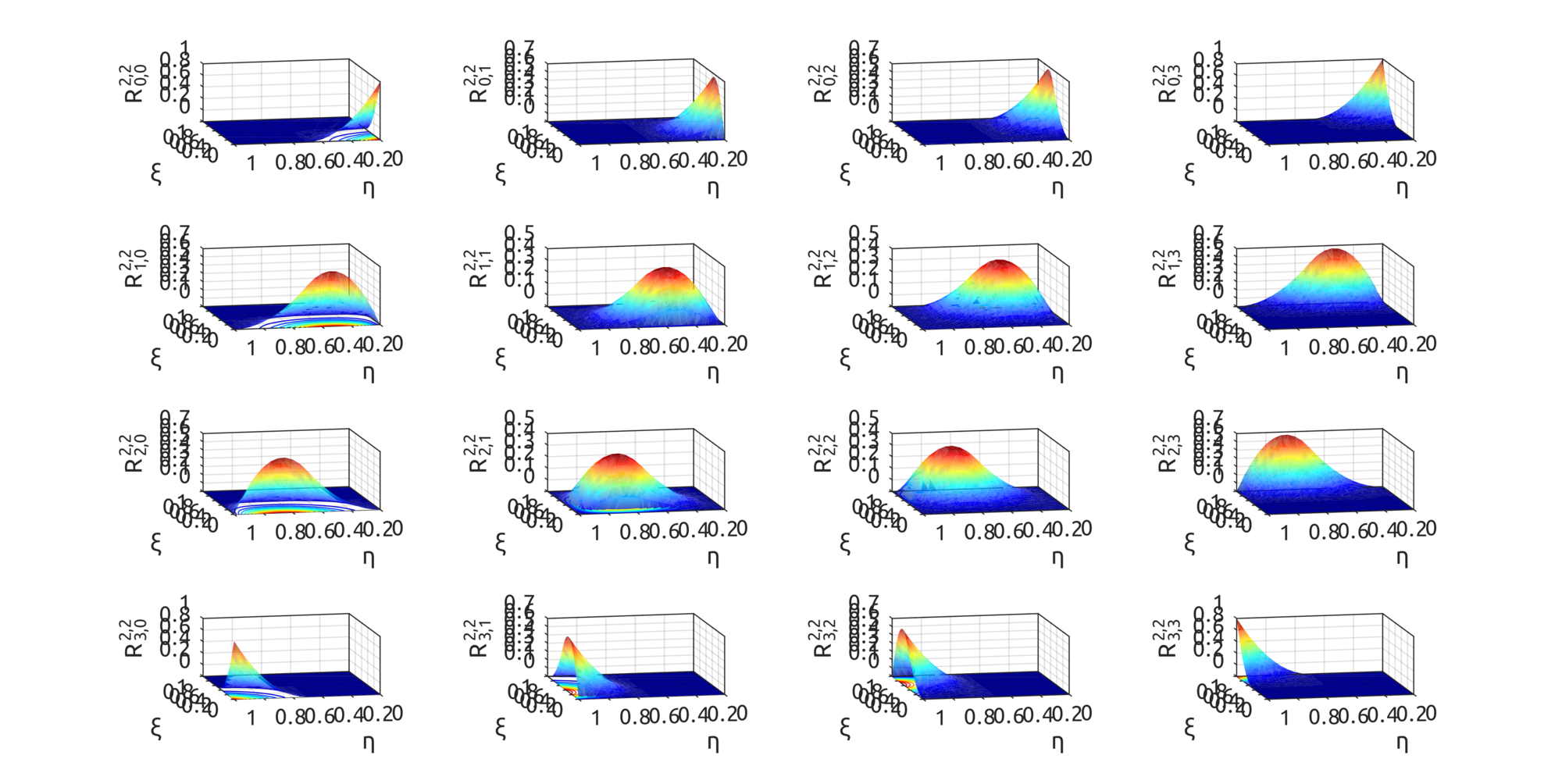
For NURBS surfaces instead we can draw bivariate basis functions. In these two examples, the first shows what happens when weights are all equal to 1, the second when weights are not all equal:



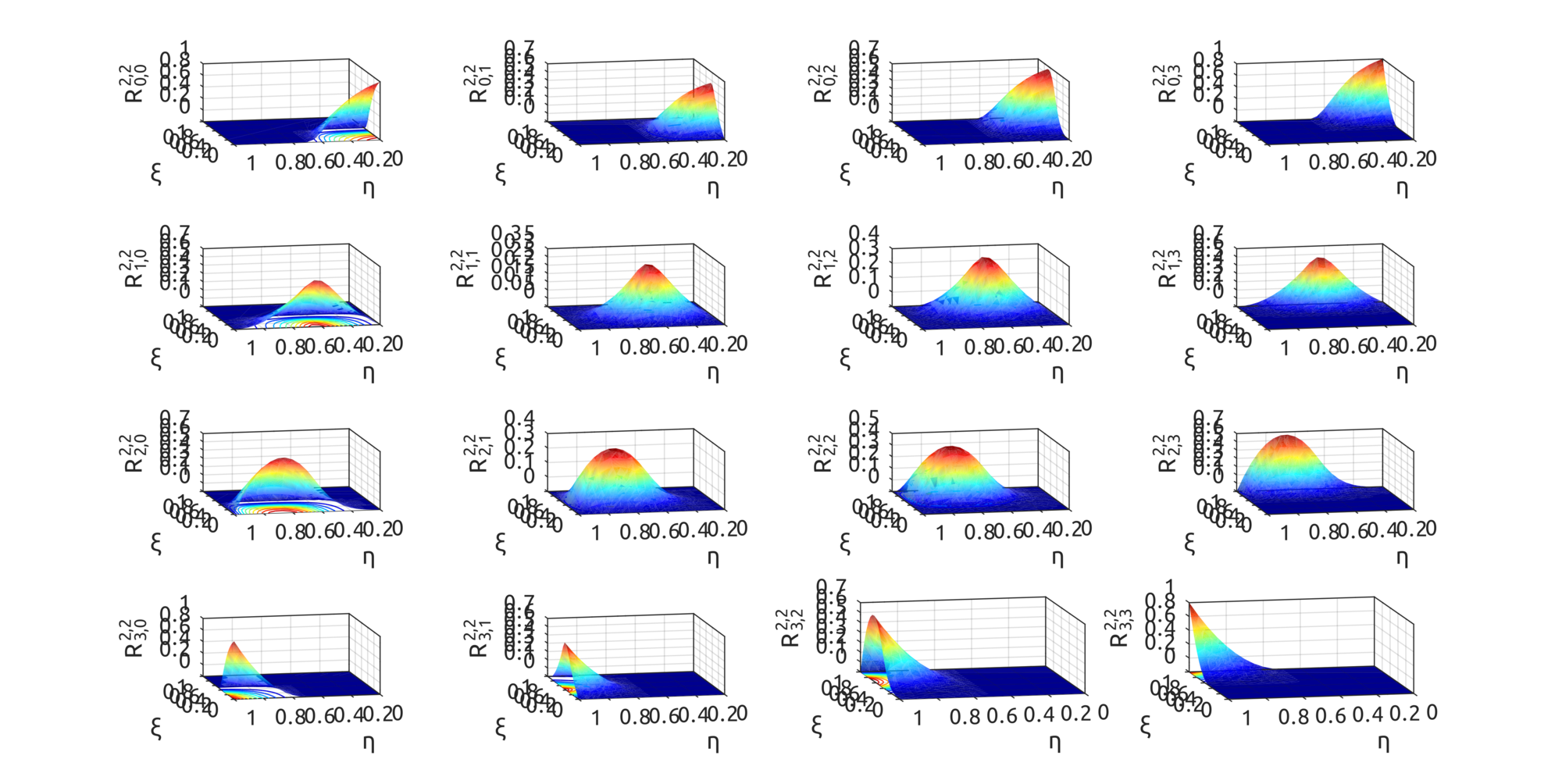
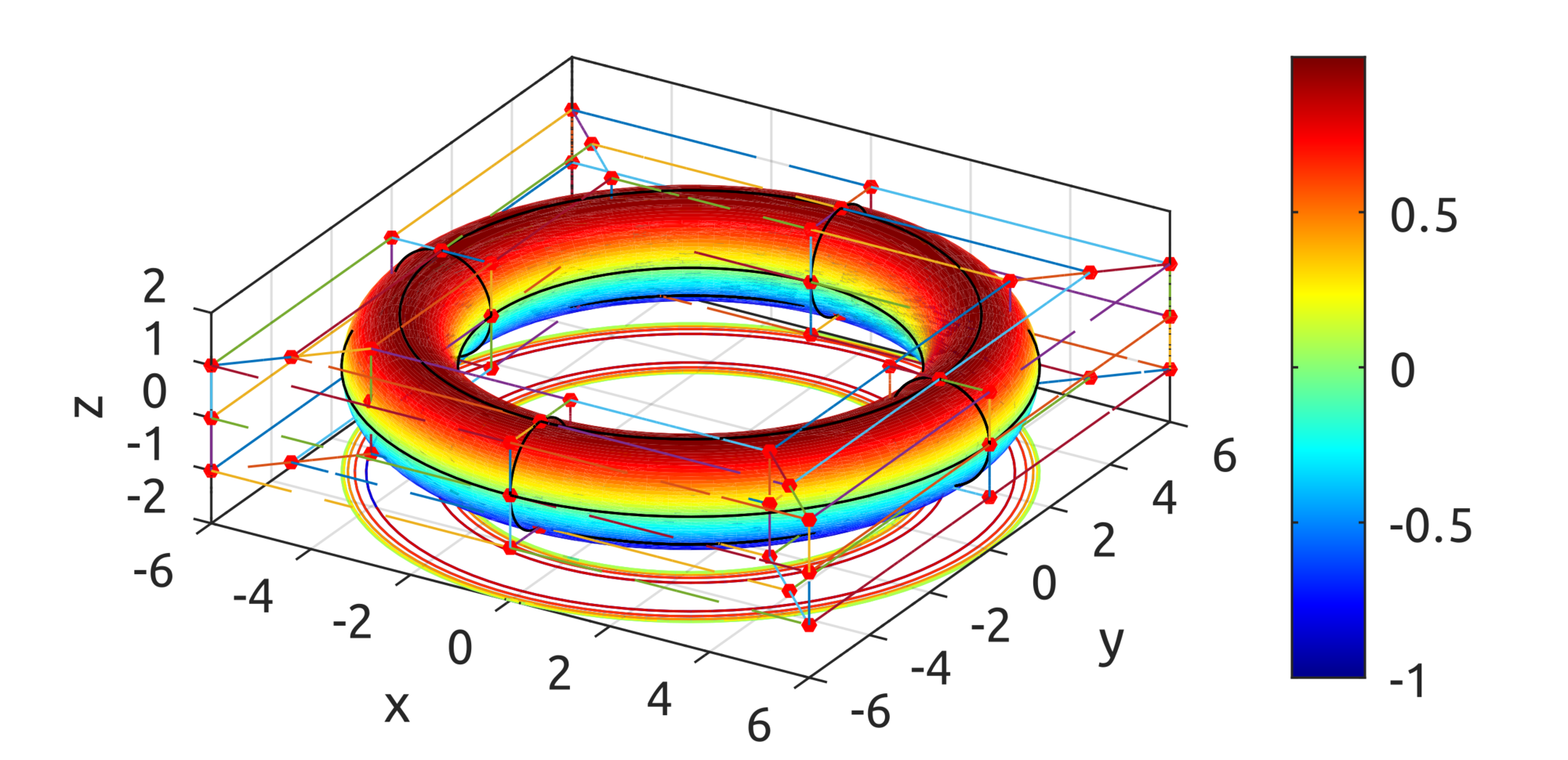
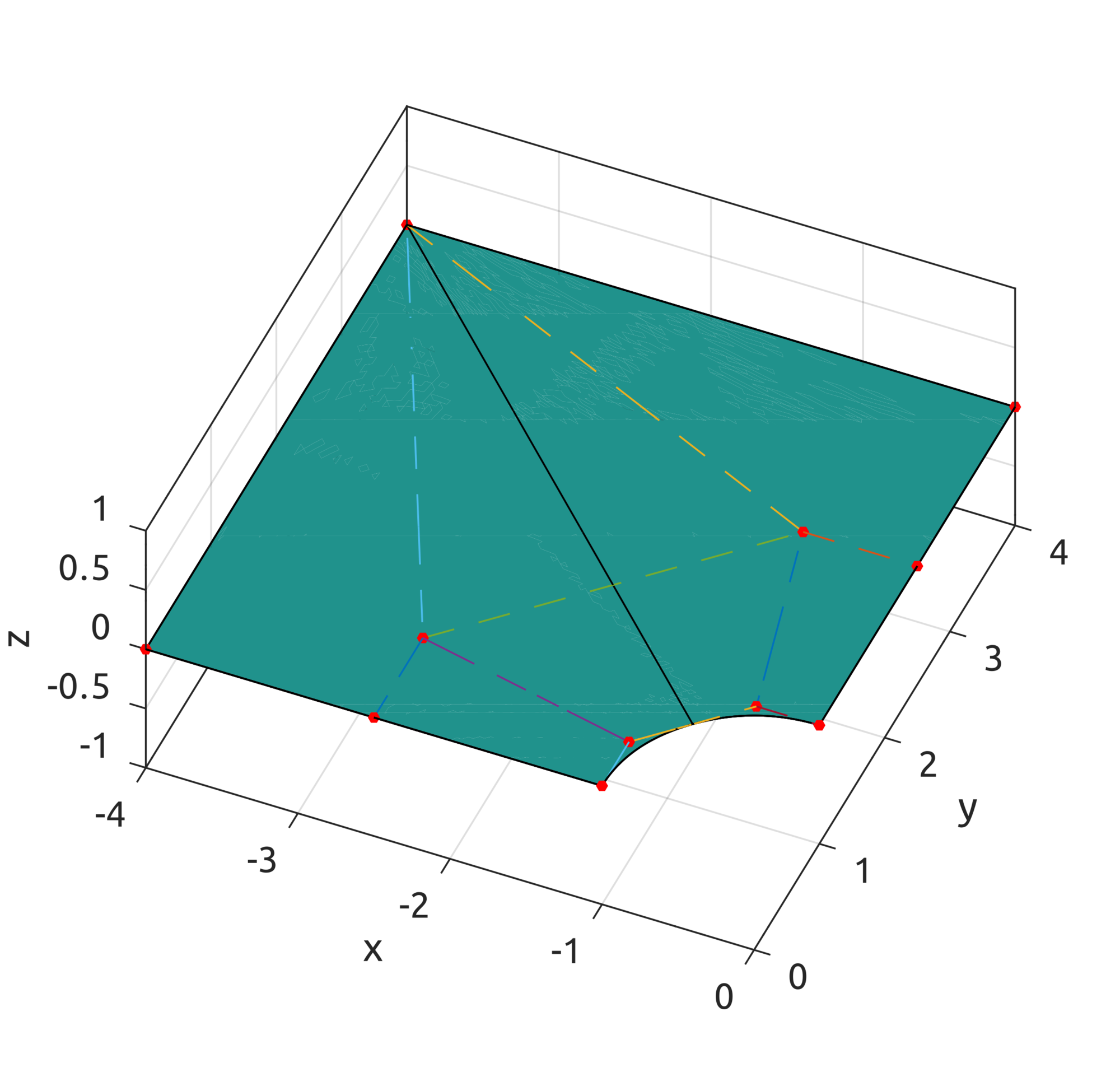
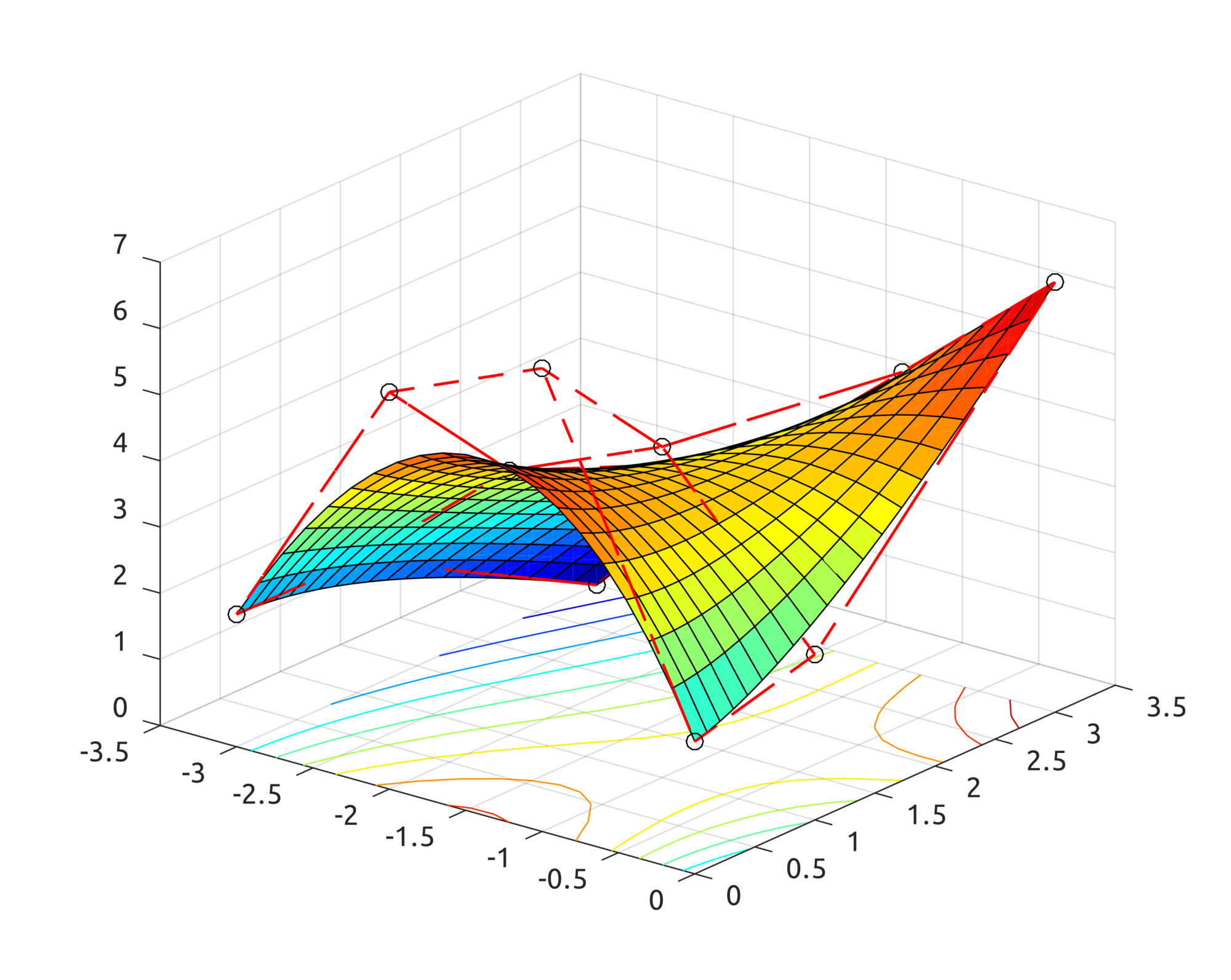
Now with the computeNURBSSurfPoint, using homogeneous coords, we can draw some interesting surfaces. Scripts are included to draw a plate with a hole:

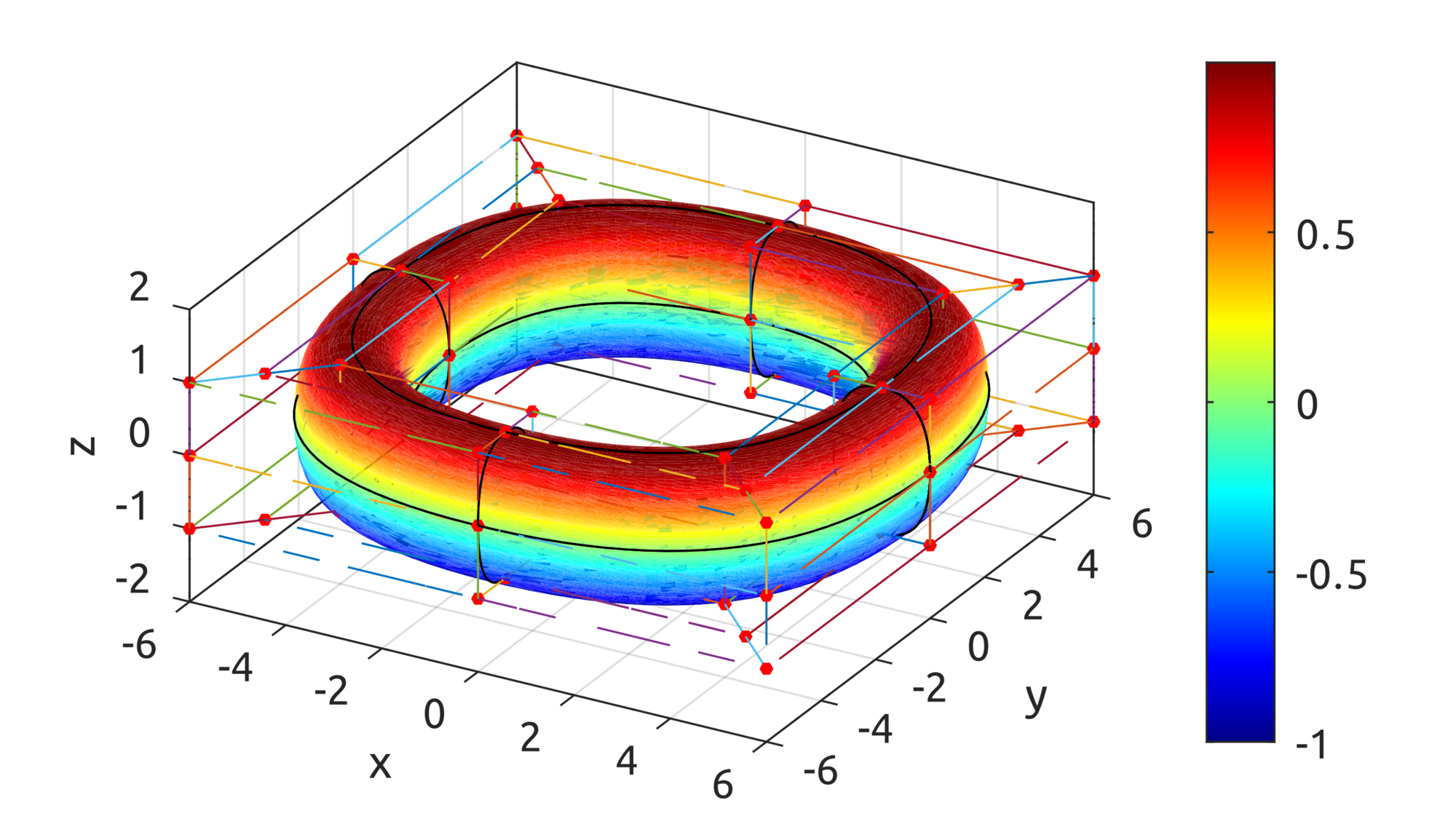
and one is provided to draw a toroid:

TypeScript Implementation

The same implementation is provided for TypeScript, so you can experiment with the browser. With the NurbsCurve you can compute NURBS basis functions:

Isogeometric Analysis: B-spline Curves and Surfaces in Octave and TypeScript

In the previous blog post here I implemented Bézier curves. There are other important structures that are used in computer graphics and I'd need those structures to define a domain and a solution in IGA for my implementation here: https://github.com/carlonluca/isogeometric-analysis.

Bézier curves are great, but the polynomials needed to describe some curves may need a high degree to satisfy multiple constraints. To overcome this problem, some structures were designed to use piecewise-polynomials instead. Examples in this case are NURBS and B-splines.

B-spline Curves

B-splines are curves that are described using piecewise-polynomials with minimal support. The parametric domain is split into multiple ranges by using a vector. The general definition of a B-spline curve is:

$$\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i},\;a\leq\xi\leq b$$
where $\boldsymbol{P}_{i}$'s are the control points of the curve and the functions $N_{i}^{p}\left(\xi\right)$ are basis functions defined as:

$$N_{i}^{0}\left(\xi\right)=\left\{ \begin{array}{ll}1, & \xi_{i}\leq\xi<\xi_{i+1}\\0,&\text{otherwise}\end{array}\right.,a\leq\xi\leq b$$ $$N_{i}^{p}\left(\xi\right)=\frac{\xi-\xi_{i}}{\xi_{i+p}-\xi_{i}}\cdot N_{i}^{p-1}\left(\xi\right)+\frac{\xi_{i+p+1}-\xi}{\xi_{i+p+1}-\xi_{i+1}}\cdot N_{i+1}^{p-1}\left(\xi\right),a\leq\xi\leq b$$
The values $\xi_{i}$ are elements of the aforementioned knot vector, defined as:

$$\Xi=\left[\underset{p+1}{\underbrace{a,\ldots,a}},\xi_{p+1},\ldots,\xi_{n},\underset{p+1}{\underbrace{b,\ldots,b}}\right],\left|\Xi\right|=n+p+2$$
where $p$ is the degree of the basis functions. A knot vector in this form is said to be nonperiodic or clamped or open.

B-spline Surfaces

By using the tensor product we can obtain B-splines in spaces of higher dimension. For surfaces, given the knot vectors:

$$\Xi=\left[\underset{p+1}{\underbrace{a_{0},\ldots,a_{0}}},\xi_{p+1},\ldots,\xi_{n},\underset{p+1}{\underbrace{b_{0},\ldots,b_{0}}}\right],\left|\Xi\right|=n+p+2$$ $$H=\left[\underset{q+1}{\underbrace{a_{1},\ldots,a_{1}}},\xi_{q+1},\ldots,\xi_{m},\underset{q+1}{\underbrace{b_{1},\ldots,b_{1}}}\right],\left|H\right|=m+q+2$$
a B-spline surface can be defined as:

$$\boldsymbol{S}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}N_{i}^{p}\left(\xi\right)N_{j}^{q}\left(\eta\right)\boldsymbol{P}_{i,j},\;\left\{ \begin{array}{c} a_{0}\leq\xi\leq b_{0}\\ a_{1}\leq\eta\leq b_{1} \end{array}\right.$$
where $p$ and $q$ are the degrees of the polynomials. In the implementations, sometimes I preferred the matrix form of the equations:

$$\boldsymbol{C}\left(\xi\right)=\left[N_{i-p}\left(\xi\right),\ldots,N_{i}\left(\xi\right)\right]\cdot\left[\begin{array}{c} \boldsymbol{P}_{i-p}\\ \vdots\\ \boldsymbol{P}_{i} \end{array}\right],\;\xi\in\left[\xi_{i},\xi_{i+1}\right)$$
For the surfaces instead, the matrix form is: $$\boldsymbol{S}\left(\xi,\eta\right)=\left[N_{i-p}\left(\xi\right),\ldots,N_{i}\left(\xi\right)\right]\cdot\left[\begin{array}{ccc} \boldsymbol{P}_{j-q,i-p} & \cdots & \boldsymbol{P}_{j-q,i}\\ \vdots & \ddots & \vdots\\ \boldsymbol{P}_{j,i-p} & \cdots & \boldsymbol{P}_{j,i} \end{array}\right]\cdot\left[\begin{array}{c} N_{j-q}\left(\eta\right)\\ \vdots\\ N_{j}\left(\eta\right) \end{array}\right],$$ $$\xi\in\left[\xi_{i},\xi_{i+1}\right),\eta\in\left[\eta_{j},\eta_{j+1}\right)$$
These forms leverage a more performant algorithm for the computation of the basis functions, which returns the value of all nonvanishing functions for a point in the parametric space. The Octave implementation is clearly simpler as Octave has native support for matrices, the TypeScript implementation instead includes a basic Matrix2 class that offers the simplest operators.

Octave Implementation

An implementation for Octave is provided in https://github.com/carlonluca/isogeometric-analysis/tree/master/3.4. There are examples to show how to draw B-spline curves with the implementation.
For example, the drawBsplineBasisFuns script shows the B-spline basis functions over the knot vector $\Xi=[0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5]$ using the provided implementation of the basis functions:

The drawBsplineCurve script draws, instead, the real curve. For example, to draw the B-spline of degree $p=2$ defined over the knot vector $\Xi=[0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1]$ with control points:

$$\boldsymbol{P}_{0}=\left(0,0,0\right),\;\boldsymbol{P}_{1}=\left(1,1,1\right),\;\boldsymbol{P}_{2}=\left(2,0.5,0\right)$$ $$\boldsymbol{P}_{3}=\left(3,0.5,0\right),\;\boldsymbol{P}_{4}=\left(0.5,1.5,0\right),\;\boldsymbol{P}_{5}=\left(1.5,0,1\right)$$

a simple call to:

drawBsplineCurve(5, 2, [
    0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1
], [
    0, 0; 1, 1; 2, 0.5; 3, 0.5; 0.5, 1.5; 1.5, 0
]);

draws:

For surfaces, drawBivariateBsplineBasisFuns can be used to draw bivariate basis functions. For example:

drawBivariateBsplineBasisFuns([
    0, 0, 0, 0.5, 1, 1, 1
], 3, 2, [
    0, 0, 0, 0.5, 1, 1, 1
], 3, 2);

gives this result:

By using the defined basis functions, data defined in https://github.com/carlonluca/isogeometric-analysis/blob/master/3.4/defineBsplineRing.m can draw a shape similar to a ring:

Note that this is not yet a toroid.

TypeScript Implementation

A TypeScript implementation is also present in the repo. With a simple code like this:

Isogeometric Analysis: Bezier Curves and Surfaces in Octave and TypeScript

While working on my sample IGA implementation here https://github.com/carlonluca/isogeometric-analysis, I found myself in need of defining and implementing the math structures used to define the domain and the solution space. This means that I had to implement various algorithms to define structures like Bezier, B-spline, NURBS and T-spline. So this is a quick intro to Bezier curves and surfaces with a couple of implementations.

Power Basis

A simple math structure to handle curves and surfaces is the power basis representation. Power basis representation uses polynomials, which are fast to compute and simple to handle.
A $n^{th}$-degree power basis curve can be defined in the parametric space as:

$$\begin{eqnarray*} \boldsymbol{C}\left(\xi\right) & = & \left(x\left(\xi\right),y\left(\xi\right),z\left(\xi\right)\right)\\ & = & \sum_{i=0}^{n}\boldsymbol{a}_{i}\xi^{i}\\ & = & \left(\left[\boldsymbol{a}_{i}\right]_{i=0}^{n}\right)^{T}\left[\xi^{i}\right]_{i=0}^{n}, \end{eqnarray*}$$

where the functions $\xi^{i}$ are the basis (or blending) functions. Using the tensor product scheme we can also define a power basis surface:

$$\begin{eqnarray*} \boldsymbol{S}\left(\xi,\eta\right) & = & \left(x\left(\xi,\eta\right),y\left(\xi,\eta\right),z\left(\xi,\eta\right)\right)\\ & = & \sum_{i=0}^{n}\sum_{j=0}^{m}\boldsymbol{a}_{i,j}\xi^{i}\eta^{j}\\ & = & \left(\left[\xi^{i}\right]_{i=0}^{n}\right)^{T}\left[\boldsymbol{a}_{i,j}\right]_{i,j=0}^{i=n,j=m}\left[\eta^{j}\right]_{j=0}^{m} \end{eqnarray*}$$

where:

$$ \left\{ \begin{array}{l} \boldsymbol{a}_{i,j}=\left(x_{i,j},y_{i,j},z_{i,j}\right)\\ b\leq\xi\leq c\\ d\leq\eta\leq e \end{array}\right.$$

Bezier

Bezier curves do not increase the space of curves representable by the power basis form, but introduce the concept of control point. Control points convey a clear geometrical meaning, which is very useful during the design process. So, a $n^{th}$-degree Bezier curve is defined as:

$$\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}B_{i}^{n}\left(\xi\right)\boldsymbol{P}_{i},\;a\leq\xi\leq b$$

where $\boldsymbol{P}_{i}$ represents the $i^{th}$ control point and:

$$B_{i}^{n}\left(\xi\right)=\frac{n!\cdot\xi^{i}\left(1-\xi\right)^{n-i}}{i!\cdot\left(n-i\right)!}$$

is the $i^{th}$ basis function (also known as Bernstein polynomial). With the tensor product scheme, we can also define a Bezier surface with:

$$\boldsymbol{S}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}B_{i}^{n}\left(\xi\right)B_{j}^{m}\left(\eta\right)\boldsymbol{P}_{i,j},\;\left\{ \begin{array}{l} a\leq\xi\leq b\\ c\leq\eta\leq d \end{array}\right.$$

Octave Implementation

In the repo https://github.com/carlonluca/isogeometric-analysis, you can find a basic implementation of Bezier curves and surfaces written for Octave (and Matlab) in: https://github.com/carlonluca/isogeometric-analysis/tree/master/3.3. The implementation is tested with a few examples. For example, given these control points:

$$\boldsymbol{P}_{0}=\left(0,0\right),\;\boldsymbol{P}_{1}=\left(1,1\right),\;\boldsymbol{P}_{2}=\left(2,0.5\right)$$ $$\boldsymbol{P}_{3}=\left(3,0.5\right),\;\boldsymbol{P}_{4}=\left(0.5,1.5\right),\;\boldsymbol{P}_{5}=\left(1.5,0\right)$$

we can get to this result by using the computeBezier.m script:

We can also define the curve in the 3D space. For example these control points:

$$\boldsymbol{P}_{0}=\left(0,0,0\right),\;\boldsymbol{P}_{1}=\left(1,1,1\right),\;\boldsymbol{P}_{2}=\left(2,0.5,0\right)$$ $$\boldsymbol{P}_{3}=\left(3,0.5,0\right),\;\boldsymbol{P}_{4}=\left(0.5,1.5,0\right),\;\boldsymbol{P}_{5}=\left(1.5,0,1\right)$$

lead to this result:

It may also be interesting to see what happens to a curve when a new control point is added to the previous one:

Another example is provided for Bezier surfaces. From these control points:

$$\boldsymbol{P}_{0}=\left(-3,0,2\right),\;\boldsymbol{P}_{1}=\left(-2,0,6\right),\;\boldsymbol{P}_{2}=\left(-1,0,7\right),\boldsymbol{P}_{3}=\left(0,0,2\right)$$ $$\boldsymbol{P}_{4}=\left(-3,1,2\right),\;\boldsymbol{P}_{5}=\left(-2,1,4\right),\;\boldsymbol{P}_{6}=\left(-1,1,5\right),\;\boldsymbol{P}_{7}=\left(0,1,2.5\right)$$ $$\boldsymbol{P}_{8}=\left(-3,3,0\right),\;\boldsymbol{P}_{9}=\left(-2,3,2.5\right),\;\boldsymbol{P}_{10}=\left(-1,3,4.5\right),\;\boldsymbol{P}_{11}=\left(0,3,6.5\right)$$

this is what the algorithms produce:

Typescript Implementation

What about a browser implemenation? The above algorithms can clearly be implemented in a browser, so this is an attempt written in TypeScript: https://github.com/carlonluca/isogeometric-analysis/tree/master/ts/src/bezier. The BezierCurve object can be used to draw a plot of the first examples:

Isogeometric Analysis and Finite Element Method

It's been some years since I completed my dissertation on FEM and Isogeometric Analysis, but I realised I never had the time to organise my code properly and archive it. So I archived a part of it in a new repo here: https://github.com/carlonluca/isogeometric-analysis. It may be useful for someone studying the topic.

The main topic of the dissertation is not the Finite Element Method (FEM) actually, but the first and the second chapters present it and I wrote a basic implementation that works for 1D problems here: https://github.com/carlonluca/isogeometric-analysis/blob/master/2.3/drawFEM1DExample.m. The first example uses the implementation to compute an approximation using FEM.

Problem

In the code, the first example solves the differential equation:

$$\left\{ \begin{array}{ll} \frac{d^{2}u(x)}{dx^{2}}=10 & \forall x\in\Omega=\left(0,1\right)\\ u(x)=0 & x=0\\ u(x)=1 & x=1 \end{array}\right.$$

Exact solution

It is possible to find an exact solution by integrating both parts twice:

$$\iint_{\Omega}u''(x)dxdx=\iint_{\Omega}10dxdx\Rightarrow u(x)=5x^{2}+c_{1}x+c_{2}$$

The solution of the system:

$$\left\{ \begin{array}{ll} u(x)=5x^{2}+c_{1}x+c_{2} & \forall x\in\Omega=\left(0,1\right)\\ u(x)=0 & x=0\\ u(x)=1 & x=1 \end{array}\right.$$

is the exact solution to the problem:

$$u(x)=x\cdot(5x-4)$$

Weak Formulation

To calculate the weak formulation we need to first define a Dirichlet lift, as the boundary conditions are non-homogeneous:

$$u(x)=\gamma(x)+v(x)\Rightarrow(\gamma(x)+v(x))''=10$$

Multiply by a test function $\varphi\in C_{0}^{\infty}(\Omega)$:

$$(\gamma(x)+v(x))''\cdot\varphi(x)=10\cdot\varphi(x)$$

Now integrate both parts:

$$\int_{\Omega}(\gamma(x)+v(x))''\cdot\varphi(x)dx=\int_{\Omega}10\cdot\varphi(x)dx$$

Using the technique of integration by parts:

$$\int_{a}^{b}u(x)v'(x)dx=\left[u(x)v(x)\right]_{a}^{b}-\int_{a}^{b}u'(x)v(x)dx$$

we can get to:

$$\left[\varphi(x)\left(\gamma(x)+v(x)\right)'\right]_{\Omega}-\int_{\Omega}\varphi'(x)\left(\gamma(x)+v(x)\right)'dx=\int_{\Omega}10\varphi(x)dx$$

$\varphi$ is a distribution and it therefore vanishes on the boundary:

$$-\int_{\Omega}\varphi'(x)\left(\gamma(x)+v(x)\right)'dx=\int_{\Omega}10\varphi(x)dx$$

It is now possible to define the two terms:

$$a(v,\varphi)=\int_{\Omega}\varphi'(x)v'(x)dx$$ $$l(\varphi)=-\int_{\Omega}\left(\varphi'(x)\gamma'(x)+10\varphi(x)\right)dx$$

Galerkin Method

At this point, the Galerkin method can be applied if we accept to look for an approximate solution in a space $V_{n}$ of dimension $dim(V_{n})=n$. Thus, assuming $\left\{ v_{i}\right\} _{i=0}^{n-1}$ is a basis for $V_{n}$, then we can write our approx solution:

$$\tilde{v}(x)=\sum_{i=0}^{n-1}\bar{v}_{i}\cdot v_{i}(x)$$

where $\left\{ \bar{v}_{i}\right\} _{i=0}^{n-1}$ are coefficients of the linear combination.
We can create a linear system with $n$ independent equations that can be written in matrix form as:

$$\boldsymbol{S}_{n}\cdot\boldsymbol{\Upsilon}_{n}=\boldsymbol{F}_{n}$$

where:

$$\boldsymbol{S}_{n}=\left[\int_{0}^{1}v_{i}v_{j}dx\right]_{i,j=0}^{n-1}$$ $$\boldsymbol{\Upsilon}_{n}=\left[\bar{v}_{i}\right]_{i=0}^{n-1}$$ $$\boldsymbol{F}_{n}=\left[-\int_{0}^{1}\left(v_{i}'(x)\gamma'(x)+10\gamma(x)\right)dx\right]_{i=0}^{n-1}$$

The basis functions $\left\{ v_{i}\right\} _{i=0}^{n-1}$ can be chosen according to the needs. In the example, simple roof functions are used: https://github.com/carlonluca/isogeometric-analysis/blob/master/2.3/computePhi.m and https://github.com/carlonluca/isogeometric-analysis/blob/master/2.3/computeDphi.m (note that nomenclature in the code is slightly different). Different approximations can be achieved with a different basis for the space $V_{n}$.
A possible choice for the Dirichlet lift is:

$$\gamma(x)=0\cdot v_{0}(x)+1\cdot v_{n-1}(x)$$

which is the one that is used in the example implementation.

Result

The example script solves the problem for $n=2,...,7$. As expected with FEM, the approximation is exact at the nodes. By increasing the dimension of the space where the solution is to be found, the approximation gets closer to the exact curve.

Lagrange Polynomials

In the previous implementation, roof functions were used. It is possible to use piecewise-polynomials of higher order. One possible implementation is Lagrange polynomials.

$$l_{Lag,i}\left(\xi\right)={\displaystyle \prod_{1\leq j\leq p_{m}+1,j\neq i}\dfrac{\left(\xi-y_{j}\right)}{\left(y_{i}-y_{j}\right)},\;i=1,2,\ldots,p_{m}+1}$$

In the repo there is a sample implementation. The demo draws Lagrange polynomials interpolating an increasing number of points: